Question

By checking work records, a carpenter finds that Juanita can build a small shed in 13 hours. Anton can do the same job in 20 hours. How long would it take to build 7 sheds if they worked together?It will take them __hour(s) __minute(s) to build 7 sheds together.

Answer 1

55 hours 9 minutes

Step-by-step explanation:

Juanita can build a small shed in 13 hours.

• Juanita's work rate = 1/13

Anton can do the same job in 20 hours.

• Anton's work rate = 1/20

Let the time taken it will take both of them to build a shed = x.

• Then, their joint rate = 1/x.

Thus:

`(1)/(13)+(1)/(20)=(1)/(x)`

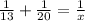
First, solve for x:

The LCM of 13 and 20 = 260.

`\begin{gathered} (20+13)/(260)=(1)/(x) \\ (33)/(260)=(1)/(x) \\ 33x=260 \\ x=(260)/(33)\; hours \end{gathered}`

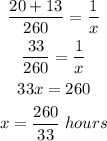
Since we want to find the time it takes to build 7 sheds if they worked together, multiply x by 7:

`\begin{gathered} 7x=7*(260)/(33) \\ =55(5)/(33)\text{ hours} \\ =55\; hours+((5)/(33)*60)\text{ minutes} \\ =55\; hours\text{ 9 minutes} \end{gathered}`

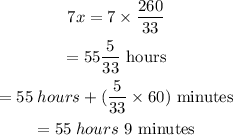
It will take them 55 hours 9 minutes to build 7 sheds together.​