Step-by-step explanation
We must answer the following question: If you draw one card at random, what is the probability that card is:
• 9. Heart?
,
• 10. 7 of diamonds?
,
• 11. face card or a club?
The total number of cards in the deck is:
• n(total) = 52.
9) The number of hearts in the deck is:
• n(heart) = 13.
The probability of drawing a heart at random is:
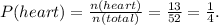
10) The number of 7 of diamonds in the deck is:
• n(7 of diamonds) = 1.
The probability of drawing a 7 of diamonds is:

11) We have the following number of cards in the deck:
• n(face card) = 3 x 4 = 12,
,
• n(club) = 13,
,
• n(face card and club) = 3.
The probability of drawing a face card or a club is given by:

Answer
9) P(heart) = 1/4
10) P(7 of diamonds) = 1/52
11) P (face card or a club) = 11/26