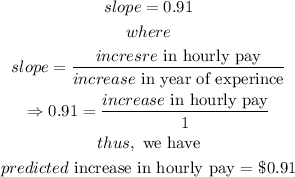Question

(THIS IS ONE QUESTION)The scatter plot shows the number of years of experience, x, and the hourly pay rate, y, for each of 24 cashiers in Florida.Use the equation of the line of best fit, =y+0.91x7.99, to answer the questions below.Give exact answers, not rounded approximations. (a) What is the predicted hourly pay rate for a cashier with 9 years of experience?$(b) What is the predicted hourly pay rate for a cashier who doesn't have any experience?$(c) For an increase of one year of experience, what is the predicted increase in the hourly pay rate?$

Answer 1

Given the scatterplot below:

where the line of best fit is expressed as

`y=0.91x+7.99`

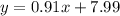
A) Predicted hourly rate for cashier with 9 years of experience:

Thus, we have

`x=9`

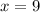
By substituting the value of 9 for x into the equation, we have

`\begin{gathered} y=0.91\left(9\right)+7.99 \\ =\$16.18 \end{gathered}`

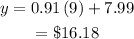
B) Predicted hourly rate for cashier with no experience:

This implies that

`x=0`

By substitution, we have

`\begin{gathered} y=0.91(0)+7.99 \\ \Rightarrow y=\$7.99 \end{gathered}`

C) Predicted increase in the hourly rate for an increase of one year of experience:

Recall that the equation of a line is expressed as

`\begin{gathered} y=mx+c \\ where \\ m\Rightarrow slope \\ m=\frac{increase\text{ in y}}{increase\text{ in x}} \end{gathered}`

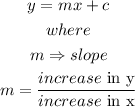
From the equation of the line of best fit, by comparison, we have

`\begin{gathered} slope=0.91 \\ where \\ slope=\frac{incresre\text{ in hourly pay}}{increase\text{ in year of experince}} \\ \Rightarrow0.91=\frac{increase\text{ in hourly pay}}{1} \\ thus,\text{ we have} \\ predicted\text{ increase in hourly pay = \$0.91} \\ \end{gathered}`