Take into account that the scalar projection is given by:
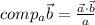
the magnitude of a vector is:
![\begin{gathered} a=\sqrt[]{(-3^{})^2+4^2} \\ a=\sqrt[]{25}=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qb1y7oxt6wa11yc9ntlymg5g1f4vipktt1.png)
The dot product between a and b is:
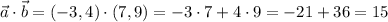
Then, the scalar projection is:

Now, consider that the vector projections is given by:

Hence, the answer is:
scalar projection of b onto a = 3
vector projection of b onto a = (-9/5 . 12/5)