Question

A couple buys a $200000 home, making a down payment of 17%. The couple finances the purchase with a 15 year mortgage at an annual rate of 3.84%. Find the monthly payment. If the couple decides to increase the monthly payment to $1300, find the number of payments.

Answer 1

First, we calculate how much is 17% of the home cost $200,00. For this, we divide 200,000 by 100 and then multiply by 17:

`(200,000)/(100)*17=34,000`

The down payment was $34,000

So we subtract this amount from the total amount of the home:

`200,000-34,000=166,000`

They still need to pay $166,000.

Now we use the mortgage formula to calculate the monthly payments "M":

`\begin{gathered} M=P*\frac{r(1+r)^n}{(1+r^{})^n-1} \\ \end{gathered}`

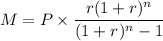
Where P is the principal or the amount borrowed. In this case:

`P=166,000`

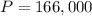
n is the number of payments. Since the payments are monthly for 15 years, and each year has 12 months. The amount of payments n is:

`n=15*12=180`

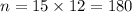
And r is the interest rate divided by 12. The interest rate is 3.84% which in decimal is 0.0384. Thus, the value of r is:

`r=(0.0384)/(12)=0.0032`

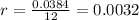
We substitute all of these values into the formula:

`M=166,000*(0.0032(1+0.0032)^(180))/((1+0.0032)^(180)-1)`

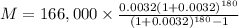
Solving the operations to find M:

`\begin{gathered} M=166,000*(0.0032(1.0032)^(180))/((1.0032)^(180)-1) \\ M=166,000*\frac{0.0032(1.7773)^{}}{1.7773^{}-1} \\ M=166,000*\frac{5.687*10^(-3)^{}}{0.7773^{}} \\ M=1,214.57 \end{gathered}`

The monthly payments: $1,214.57

If they increase the monthly payment to 1300, we need to divide the 166,000 by 1,300 to find the number of payments they have to make:

`(166,000)/(1300)=127.7`

The number of payments: 127.7