The cost of gas will be called "x", while the cost of electricity will be called "y". On the first month he spent 150 units of gas and 520 units of electricity and got a bill of 84.20, therefore:
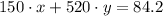
On the next month he spent 210 units of gas and 405 units of electricity getting a bill of 82.35, therefore:
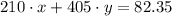
We can form a system of equations with these two expressions, we have:
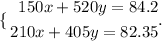
To solve it we will isolate the "x" variable on the first equation, we have:
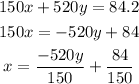
We can now use this value on the place of "x" on the second equation.
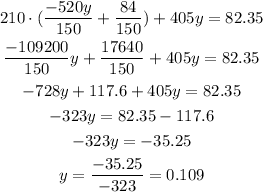
We can use this value of y on one of the equations before to find x. We have:
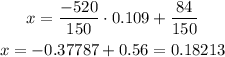
The cost of gas is 0.18213 per unit and the cost of electricity is 0.109 per unit.