Question

Please answer the following question correctly. If the question stated isn’t clear, it states:*In the figure below, the segments EF and EG are tangent to the circle centered at 0. Given thatEG=2.8 and OE =3.5, find OF.*

Answer 1

Given:

EG = 2.8, OE = 3.5,

Required: OF

To solve this problem, we need to apply this rule:

The tangent is always perpendicular to the radius drawn to the point of tangency.

Hence, we can draw:

Let the length of OF be r

Using Pythagoras theorem, we can solve for r

`\begin{gathered} hypothenuse^2\text{ = opposite}^2\text{ + adjacent}^2 \\ 3.5^2\text{ = r}^2+\text{ 2.8}^2 \\ r^2\text{ = 4.41} \\ r\text{ = 2.1} \end{gathered}`

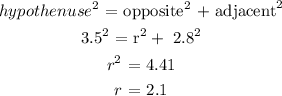
Hence, the length of OF is 2.1