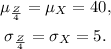Question

6-18.

Consider a random variable X with Mx = 40 and 0x = 5. Let Z=X+X+X+x.
a. Find uz and oz.
b. What does X+X+X+X represent?
What does 1/4 (X+X+X+X) represent?
d.Find mean 1/4z and variance 1/4z

Answer 1

In this problem, we consider the probability distribution of a random variable X with:

• mean value μ_X = 40,

,

• standard deviation σ_X = 5.

Now, we consider the random variable Z defined as:

`Z=X+X+X+X=4X\text{.}`

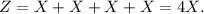
a. From probability theory, we know that a linear transformation of the type:

`X\rightarrow Z=a+b\cdot X,`

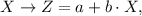
changes the mean value and the standard deviation in the following way:

`\begin{gathered} \mu_X\rightarrow\mu_Z=a+b\cdot\mu_X, \\ \sigma_X\rightarrow\sigma_Z=b\cdot\sigma_X\text{.} \end{gathered}`

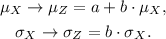
In this case, we have a = 0 and b = 4, so we have that:

`\begin{gathered} \mu_X\rightarrow\mu_Z=0+4\cdot\mu_X=4\cdot40=160, \\ \sigma_X\rightarrow\sigma_Z=4\cdot\sigma_X=4\cdot5=20\text{.} \end{gathered}`

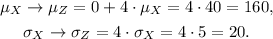
b. The sum Z = X + X + X + X = 4X represents a new random variable that is 4 times the original random variable X. So Z is a random variable obtained from a specific linear transformation of the original random variable X.

c. Because (X + X + X + X)/4 = X, this sum represents just the original random variable X.

d. To compute μ_Z/4 and σ_z/4, we take into account that:

`U=(Z)/(4)=((4X))/(4)=X\text{.}`

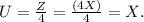
So the values of μ_Z/4 and σ_z/4 are just:

`\begin{gathered} \mu_{(Z)/(4)}=\mu_X=40, \\ \sigma_{(Z)/(4)}=\sigma_X=5. \end{gathered}`

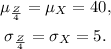
Answers

a.

`\begin{gathered} \mu_Z=160, \\ \sigma_X=20. \end{gathered}`

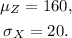
b. The sum Z = X + X + X + X = 4X represents a new random variable that is 4 times the original random variable X. So Z is a random variable obtained from a specific linear transformation of the original random variable X.

c. Because (X + X + X + X)/4 = X, this sum represents just the original random variable X.

d.

`\begin{gathered} \mu_{(Z)/(4)}=\mu_X=40, \\ \sigma_{(Z)/(4)}=\sigma_X=5. \end{gathered}`