Question

3. FG has an endpoint G at (-4,6). If the midpoint of the line segment is ( 1, 1), what are the coordinates of F?

Answer 1

midpoint= (1, 1)

Xm = 1 Ym = 1

G( -4, 6)

This implies that;

x₂= -4 y₂ = 6

Let the coordinates of F by (x₁ y₁)

`x_m=(x_1+x_2)/(2)`

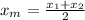
Xm = 1 x₂= -4

substitute in the above and then solve for x₁

That is;

`1=(x_1-4)/(2)`

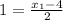
2 = x₁ - 4

add 4 to both-side of the equation

6 = x₁

x₁=6

Similarly;

`y_m=(y_1+y_2)/(2)`

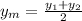
Ym= 1 y₂= 6

substitute the value in the above and solve for y₁

That is;

`1=(y_1+6)/(2)`

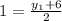
2= y₁ + 6

subtract 6 from both-side of the equation

2-6 =y₁

-4 = y₁

y₁= -4

The coordinates of F are ( 6, -4)