Question

200 lottery tickets are sold for $4 each. The person with the single winning ticket will get $71. What is the expected value for a ticket in this lottery?

Answer 1

From the information given, we have the following;

`\begin{gathered} \text{Cost of ticket}=4 \\ \text{Number of tickets}=200 \\ \text{ Winning prize}=71 \end{gathered}`

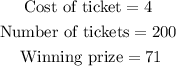
Therefore, we can deduce the following;

`\begin{gathered} P\lbrack\text{ winning\rbrack}=(1)/(200) \\ P\lbrack lo\sin g\rbrack=(199)/(200) \\ \text{ Gain/loss of winning}=67\text{ (that is \$71-\$4)} \\ \text{ Gain/loss of losing}=-4 \end{gathered}`

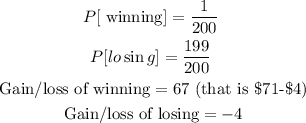
Therefore, the expected value shall be calculated as follows;

`\begin{gathered} Expected\text{ value}=(P\lbrack\text{ winning\rbrack{}x Gain/loss of winning})+(P\lbrack lo\sin g\rbrack*\text{ Gain/loss of losing} \\ Exp\text{ected value}=((1)/(200)*(67)/(1))+((199)/(200)*\lbrack-4\rbrack) \\ EV=(67)/(200)-(796)/(200) \\ EV=-(729)/(200) \\ EV=-3.645 \\ \text{Expected value}\approx-3.65\text{ (rounded to the nearest hundredth)} \end{gathered}`

ANSWER:

The expected value of a ticket in this this lottery is -$3.65 (rounded to the nearest hundredth).