Given data:
* The length of the pendulum is,
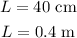
* The angle of the pendulum with the y-axis is,
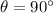
Solution:
The angular acceleration of the pendulum in terms of the length is,
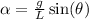
Substituting the known values,
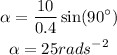
Thus, the angular acceleration of the pendulum is 25 radians per second squared.
Hence, the third option is the correct answer.