Step-by-step explanation
By definition, a prime number is a natural number greater than 1 that is not a product of two smaller natural numbers.
We must show that 17 is the only prime number x that can be written as:

We can rewrite this expression as:
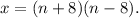
1) If n = -8 or n = +8, we have:
![x=(n+8)(n-8)=0<1\text{ ^^^^2716},]()
2) If -8 < n < 8, we have:
![n+8>0\text{ and }n-8<0\Rightarrow x<0<1\text{ ^^^^2716}]()
3) If n < -8 or n > 8, we have:
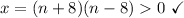
4) By assumming n < -8 or n > 8, x is a primer number only if (n + 8) or (n - 8) is a ±1.
For both cases, we have:
![\begin{gathered} \text{If }n+8=1\Rightarrow n=-7\Rightarrow(n-8)=-15\Rightarrow x=(n+8)(n-8)=-15<0\text{ ^^^^2716} \\ \text{If }n+8=-1\Rightarrow n=-7\Rightarrow(n-8)=-1\Rightarrow x=(n+8)(n-8)=17>0\text{ }✓. \end{gathered}]()
So the only possibility is to have x = 17.
5) We know that 17 is a prime because it is only divisible by 1 and 17.
Answer
We rewrite the expression as:
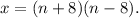
1) If n = -8 or n = +8, we have:
![x=(n+8)(n-8)=0<1\text{ ^^^^2716},]()
2) If -8 < n < 8, we have:
![n+8>0\text{ and }n-8<0\Rightarrow x<0<1\text{ ^^^^2716}]()
3) If n < -8 or n > 8, we have:
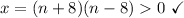
4) By assumming n < -8 or n > 8, x is a primer number only if (n + 8) or (n - 8) is a ±1.
For both cases, we have:
![\begin{gathered} \text{If }n+8=1\Rightarrow n=-7\Rightarrow(n-8)=-15\Rightarrow x=(n+8)(n-8)=-15<0\text{ ^^^^2716} \\ \text{If }n+8=-1\Rightarrow n=-7\Rightarrow(n-8)=-1\Rightarrow x=(n+8)(n-8)=17>0\text{ }✓. \end{gathered}]()
So the only possibility is to have x = 17.
5) We know that 17 is a prime because it is only divisible by 1 and 17.