After dilation, the area of the resulting shape is equal to the product between the area of the original shape and the square of the scale factor:
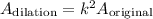
The area of the original shape is 25 ft² and the scale factor is k=3.5, so the area of the shape after the dilation can be determined as:
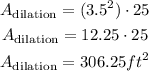
After the dilation, the area will be 306.25 ft²