Question

Find the equation for the line (5,5) and ( 1,-1)

Answer 1

Concept:

The formula to calculate the equation of a line is given below as

`(y_2-y_1)/(x_2-x_1)=(y-y_1)/(x-x_1)`

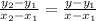
The coordinates given in the question are

`\begin{gathered} (x_1,y_1)\Rightarrow(5,5) \\ (x_2,y_2)\Rightarrow(1,-1) \end{gathered}`

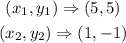
By substituing the values in the formula above, we will have

`\begin{gathered} (y_(2)-y_(1))/(x_(2)-x_(1))=(y-y_(1))/(x-x_(1)) \\ (-1-5)/(1-5)=(y-5)/(x-5) \\ -(6)/(-4)=(y-5)/(x-5) \\ (3)/(2)=(y-5)/(x-5) \\ \end{gathered}`

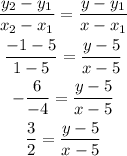
Cross multiply, we will have

`\begin{gathered} (3)/(2)=(y-5)/(x-5) \\ 2(y-5)=3(x-5) \\ 2y-10=3x-15 \\ 2y=3x-15+10 \\ 2y=3x-5 \\ divide\text{ ball through by 2} \\ (2y)/(2)=(3x)/(2)-(5)/(2) \\ y=(3)/(2)x-(5)/(2) \end{gathered}`

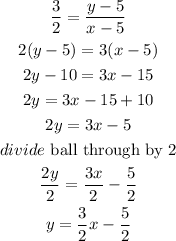
Hence,

The equation of the line is given below as

`\Rightarrow y=(3)/(2)x-(5)/(2)`