Therefore, the exact values of the six trigonometric functions at
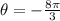 are:
are:
![\[\sin \theta = -(√(3))/(2), \cos \theta = -(1)/(2), \tan \theta = -√(3), \csc \theta = -(2)/(√(3)), \sec \theta = -2, \cot \theta = -(1)/(√(3))\]](https://img.qammunity.org/2023/formulas/mathematics/college/im845ppiizd5bu5r0b5ddo6dj53hjps782.png)
Given:
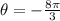
Part A: Coterminal Angle of
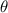 such that
such that
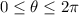
To find the coterminal angle within the range \(0 \leq \theta \leq 2\pi\), let's add
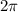 to
to
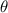 until we obtain an angle within the desired range:
until we obtain an angle within the desired range:
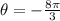
Adding
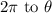 :
:
![\[\theta_{\text{co-terminal}} = -(8\pi)/(3) + 2\pi = -(8\pi)/(3) + (6\pi)/(3) = -(2\pi)/(3)\]](https://img.qammunity.org/2023/formulas/mathematics/college/lj5fpwpdgdxn7chrdtl89weyzey20re0pc.png)
Therefore, a coterminal angle of
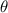 such that
such that
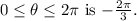
Part B: Exact Values of Trigonometric Functions at
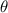
To find the exact values of the trigonometric functions at
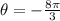 , we can use the properties of trigonometric functions related to the unit circle.
, we can use the properties of trigonometric functions related to the unit circle.
Given
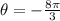 , which is in the third quadrant (since it is more than
, which is in the third quadrant (since it is more than
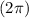 :
:
Let's evaluate the trigonometric functions at this angle:
Given:
- Sine
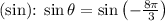
- Cosine
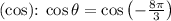
- Tangent
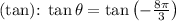
- Cosecant
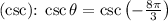
- Secant
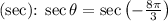
- Cotangent
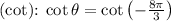
Let's calculate these values using the properties of trigonometric functions and the unit circle:
The reference angle for
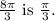 In the third quadrant, sine and cosine are negative:
In the third quadrant, sine and cosine are negative:
![\[\sin \theta = -\sin\left((\pi)/(3)\right) = -(√(3))/(2)\]](https://img.qammunity.org/2023/formulas/mathematics/college/28nz4vdwpz5420qk7x8t047ra4tq7cgitm.png)
![\[\cos \theta = -\cos\left((\pi)/(3)\right) = -(1)/(2)\]](https://img.qammunity.org/2023/formulas/mathematics/college/hojokl8njypefqv7oupxv5izqvxrqqzrwe.png)
![\[\tan \theta = \tan\left((\pi)/(3)\right) = -√(3)\]](https://img.qammunity.org/2023/formulas/mathematics/college/21j242630kaagkxjorogodfzgojorzs1lr.png)
![\[\csc \theta = -(1)/(\sin \theta) = -(2)/(√(3))\]](https://img.qammunity.org/2023/formulas/mathematics/college/o951zbsi39gamnv53kjjhk08fskr5ozl40.png)
![\[\sec \theta = -(1)/(\cos \theta) = -2\]](https://img.qammunity.org/2023/formulas/mathematics/college/lwqesaq4nihatbddme63cse92hwz2xqepm.png)
![\[\cot \theta = -(1)/(\tan \theta) = -(1)/(√(3))\]](https://img.qammunity.org/2023/formulas/mathematics/college/mx06p51ed24dqx4b7t85ptznaxiygz8ijg.png)