Step-by-step explanation
Let's picture the situation of the exercise:
We're looking for the value of the height of the tree; namely, for the value of h in the drawing. Laying down the drawing, we get
Since both triangles are similar, we can apply the Geometric Mean theorem, which says that
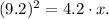
Solving this equation for x, we get
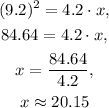
However, note that
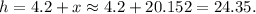
Now, since the second decimal place of our approximation of h is exactly 5, the rounding rule says that we must eliminate 5 and add one to the tenths, to get 24.2.
Answer
The height of the tree is (approximately) 24.2 ft.