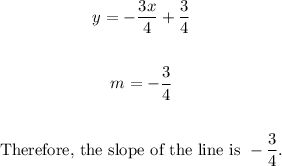1 Answer

Sommmen · Answer 1 · 2023-05-12T23:25:31+0000

The slope-intercept form of an equation is written as

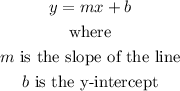
$\begin{gathered} y=mx+b \\ \text{where} \\ m\text{ is the slope of the line} \\ b\text{ is the y-intercept} \end{gathered}$

Given the equation

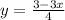
Separate the fraction so that it is expressed in two terms.

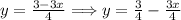
$y=(3-3x)/(4)\Longrightarrow y=(3)/(4)-(3x)/(4)$

Swap the two position of the two terms

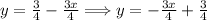
$y=(3)/(4)-(3x)/(4)\Longrightarrow y=-(3x)/(4)+(3)/(4)$

Now that it is in the slope-intercept form, we can observe that the slope of the line is

$\begin{gathered} y=-(3x)/(4)+(3)/(4) \\ \\ m=-(3)/(4) \\ \\ \text{Therefore, the slope of the line is }-(3)/(4)\text{.} \end{gathered}$

Please log in or register to add a comment.