Question

Suppose that in a small town of 20 people one person earns 90,000 per year and the other 19 each earn 20,000 which is the better measure of the center the mean or the median

Answer 1

We know that in a small town of 20 people one person earns 90,000 per year and the other 19 each earn 20,000.

We must determine which is the better measure of the center.

We have the options:

1. Mean

`\bar{x}=(90000+19(20000))/(20)=23500`

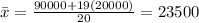
2. Median

`M=20000`

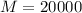
In order to take the best option we must take into account that there are 19 people who earn 20000 and only one person who earns 90000.

That means that person who earns 90000 is an outlier.

The median is a better measure of the "center" than the mean because 19 of the values are 20000 and one is 90000. The 90000 is an outlier. The 20000 gives us a better sense of the middle of the data.

ANSWER:

Option 3. The median.