Question

consider the arithmetic sequence whose first few entries are 6,11,16,21,26,31 Part A.) determine the 100th entry in the sequence, and explain why your answer is correct. Part B.) find an expression for the nth entry in the sequence, and explain in detail why your expression is valid. Part C.) is 1000 in entry in the sequence? If yes, which entry? If no, why not? Determine the answer to these questions in two ways: with Algebra and in a way that a student in elementary school might be able to. Part D.) is 201 an entry in the sequence? If yes, which entry? If no, why not? Determine the answer to these questions in to ways: with Algebra and in a way that a student in elementary school might be able to.

Answer 1

A)

The arithmetic sequence is modeled by the following equation:

`a_n=a_1+(n-1)r`

Where a_n is the nth term, a_1 is the first term and r is the rate.

We can see in the sequence that the first term is 6, and each number is the previous number plus 5, so the rate of our sequence is 5.

So, in order to find the 100th term, let's use n = 100 in our equation:

`\begin{gathered} a_(100)=a_1+(100-1)\cdot5 \\ a_(100)=6+99\cdot5 \\ a_(100)=6+495=501 \end{gathered}`

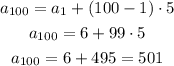
So the 100th term is 501.

B) The expression for the nth term is the general expression used for arithmetic sequences:

`a_n=a_1+(n-1)r`

We can find this expression generalizing the following equations:

`\begin{gathered} a_2=a_1+r \\ a_3=a_2+r=a_1+2\cdot r \\ a_4=a_3+r=a_1+3\cdot r \\ \ldots \\ a_n=a_(n-1)+r=a_1+(n-1)\cdot r \end{gathered}`

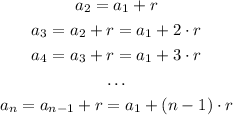
C)

In order to check if 1000 is an entry in the sequence, we can use the value of a_n = 1000 and try to find the value of n:

`\begin{gathered} 1000=6+(n-1)\cdot5 \\ 1000=6+5n-5 \\ 5n=1000-6+5 \\ 5n=999 \\ n=199.8 \end{gathered}`

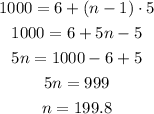
Our value of n is not a whole number, so the entry 1000 is not a valid entry.

We can also see in our sequence that the last digit is always 6 or 1. So checking the entry 1000, the last digit is 0, so we know that this is not a valid entry.

D)

In order to check if 201 is an entry in the sequence, we can use the value of a_n = 201 and try to find the value of n:

`\begin{gathered} 201=6+(n-1)\cdot5 \\ 201=6+5n-5 \\ 5n=201-6+5 \\ 5n=200 \\ n=40 \end{gathered}`

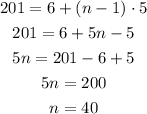
Our value of n is a whole number, so the entry 201 is a valid entry.

All numbers in our sequence ends with 1 or 6. So, checking the entry 201, the last digit is 1, therefore we know that this is a valid entry.