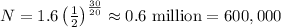It is given that the half-life is 20 years and the current population is 1.6 million.
It is required to find the population in 30 and 65 years, respectively.
Recall the Exponential Decay Half-Life Formula:
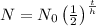
Where N₀ is the current population, t is the time in years, and h is the half-life.
(a) Substitute N₀=1.6, h=20, and t=30 into the formula:
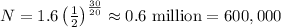
About 600,000 animals will be left in 30 years.
(b) Substitute N₀=1.6, h=20, and t=65 into the formula: