Given data
*The given mass of the box is m = 4 kg
*The given frictionless table of height is h = 0.2 m
*The spring compressed at a distance is x = 0.06 m
*The table landing a distance is d = 1.2 m
(b)
The formula for the time taken by the box is given by the equation of motion as
![\begin{gathered} h=(1)/(2)gt^2 \\ t=\sqrt[]{(2h)/(g)} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/oe7enbxzshecmxg5oyzrjyjfzsfy41vygb.png)
Substitute the known values in the above expression as
![\begin{gathered} t=\sqrt[]{(2*0.2)/(9.8)} \\ =0.202\text{ s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/huanomu6lwzi06660k0elyjpdmcf2d9lrh.png)
The formula for the box's speed at the instant it leaves the table is given as
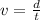
Substitute the known values in the above expression as
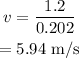
Hence, the box's speed at the instant it leaves the table is v = 5.94 m/s
(d)
The formula for the spring constant is given by the conservation of energy as
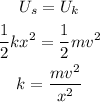
*Here U_s is the spring energy
*Here U_k is the kinetic energy
Substitute the known values in the above expression as
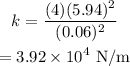
Hence, the spring constant is k = 3.92 × 10^4 N/m
(c)
The formula for the energy initially stored in the spring is given as
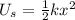
Substitute the known values in the above expression as
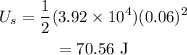
Hence, the energy initially stored in the spring is U_s = 70.56 J