Answer:
Question:
The equation of a line has a y-intercept of 2 and a slope of 1/2. Which of the following is not true about the line?
Concept:
The general equation of a line in slope-intercept form is given below as

By substituting the values, we will have that the equation of the line will be
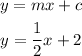
Hence,
The equation of the line in slope intercept form is y=1/2x+2 (TRUE)
Step 2:
To figure out if the point (4,6) lies on the line, we will substitute the value of x=4 to get the value of y=6

Step 3:
To figure out if the point (20,12) lies on the line, we wil substitute the value of x=20 to get the value of y =12
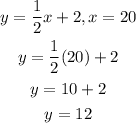
Step 4:
The graph of the function is given below as
From the image above, we can see that the line will never pass through quadrant 4
Hence,
The final answer is
The point (4,6) is on the line (not true)