Vertex form of Parabolas
Initial explanation
We want to write the following parabola in the vertex form equation:
x² - 12x + y + 40 = 0
↓ taking x², - 12x and 40 to the right side
y = -x² + 12x - 40
This means that we want to transform our equation into another equation like this:

where a, h and k are numbers.
In order to do so we rewrite the equation completing the square.
Step 1: finding a
We rewrite our equation so the first term is positive:
y = -x² + 12x - 40
↓
y = -(x² - 12x + 40)
Step 2: finding h
We want to rewrite x² - 12x + 40 completing the square.
We know that:
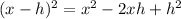
Since 2 · 6 = 12, then in this case, we have that:
x² - 12x + 40 = x² - 2 · 6x + 40
Then, in this case h = 6
Since
h² = 6² = 36
we add and subtract 36 in our question:
x² - 2 · 6x + 40 = x² - 2 · 6x + (36 - 36) + 40
we are going to use the terms that form the square:
x² - 2 · 6x + 36 - 36 + 40
= [x² - 2 · 6x + 36] - 36 + 40
↓ since -36 + 40 = 4
= [x² - 2 · 6x + 36] + 4
Since
(x - 6)² = [x² - 2 · 6x + 36]
then
[x² - 2 · 6x + 36] + 4
= (x - 6)² + 4
Step 3: finding the final equation
Then, we have that
y = -(x² - 12x + 40)
where, we found that in square form:
x² - 12x + 40 = (x - 6)² + 4
Then, replacing it, we have
y = -(x² - 12x + 40)
↓replacing (x - 6)² = [x² - 2 · 6x + 36]
y = -((x - 6)² + 4)
↓multiplying -1
y = -(x - 6)² - 4
Then, we have found an equation of the vertex form for this parabola.
Answer: y = -(x - 6)² - 4