Question

Hello. Im trying to help my 9th grade daughter who is autistic do her test corrections. It has been over 20 yrs since I had Algebra 1 so Im very rusty. She easily gets friends so Im trying to do the leg work before going over it with her. Thank you so much in advance

Answer 1

To answer this question, we know that the recursive formula for the sequence is:

`a_n=(1)/(2)(a_(n-1)),a_1=86_{}`

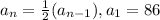
With this formula, we can obtain the second term as follows:

`a_2=(1)/(2)(a_(2-1))\Rightarrow a_2=(1)/(2)a_1\Rightarrow a_1=86\Rightarrow a_2=(1)/(2)86\Rightarrow a_2=43`

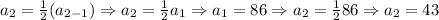
The third term of the sequence is:

`a_3=(1)/(2)(a_(3-1))\Rightarrow a_3=(1)/(2)(a_2)\Rightarrow a_3=(1)/(2)43\Rightarrow a_3=21.5`

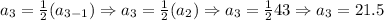
The fourth term of the sequence is:

`a_4=(1)/(2)(a_(4-1))\Rightarrow a_4=(1)/(2)a_3\Rightarrow a_4=(1)/(2)21.5\Rightarrow a_4=10.75`

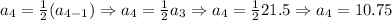
We needed to find these terms to check the type of sequence we have here. Since we have that the ratio between the second term and the first term is the same as the third term and second term, and so on, we have:

`(43)/(86)=(21.5)/(43)=(10.75)/(21.5)=(1)/(2)`

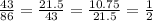
Then, we have here a geometric sequence. The common ratio here is r = 1/2.

Then, if we know that the explicit formula for a geometric sequence is of the form:

`a_n=a_1\cdot r^(n-1)`

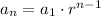
Since we have that:

`\begin{cases}a_1=86 \\ r=(1)/(2)\end{cases}`

Then, we have:

`a_n=86\cdot((1)/(2))^(n-1)`

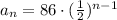
We can check this result if we calculate the values for the first, second, third, and fourth terms above:

`a_1=86\cdot((1)/(2))^(1-1)=86\cdot1=86`

`a_2=86\cdot((1)/(2))^(2-1)=86\cdot(1)/(2)=43`

`a_3=86\cdot((1)/(2))^(3-1)=86\cdot((1)/(2))^2=86\cdot(1)/(4)=21.5`

`a_4=86\cdot((1)/(2))^(4-1)=86\cdot((1)/(2))^3=86\cdot((1)/(8))=10.75`

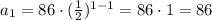
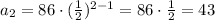
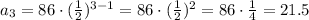
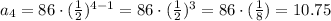
In summary, we have that the explicit formula is:

`a_n=86\cdot((1)/(2))^(n-1)`

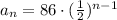
Where the common ratio is r = 1/2.