The function is to have asymptotes at the line:
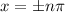
The graph will have an asymptote when the denominator is 0.
By this definition, the graph of cos x has no asymptotes.
We know that:

Therefore, the functions where sin x is at the denominator will have asymptotes at x = π.
The remaining functions can be written as follows:
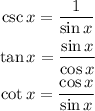
Therefore, the functions with the asymptote at x = π are csc x and cot x.
OPTION B is the correct answer.