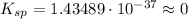Question

Calculate the ksp value for Fe(OH)3 given that that solubility is 2.7x10^-10mol/L

Answer 1

So,

We could use the following reaction to find the Ksp value:

`Fe(OH)_(3(s))\leftrightarrow1Fe^(3+)_((aq))+3(OH)^-_((aq))`

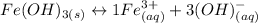
We know that the solubility of Fe(OH)3 is:

`(2.7\cdot10^(-10)molFe(OH)_3)/(L)`

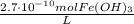
As you can notice, we could find the concentrations of each ion formed in the products using the stoichiometry of the reaction:

`\begin{gathered} \lbrack Fe^(3+)\rbrack=(2.7\cdot10^(-10)molFe(OH)_3)/(L)\cdot\frac{1molFe^(3+)}{1^{}molFe(OH)_3}^{} \\ \lbrack Fe^(3+)\rbrack=\frac{2.7\cdot10^(-10)molFe^(3+)_{}}{L} \end{gathered}`

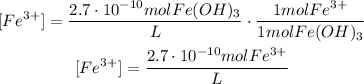
And now, we could do the same thing to find the concentration of the [OH]- ions:

`\begin{gathered} \lbrack OH\rbrack^-=(2.7\cdot10^(-10)molFe(OH)_3)/(L)\cdot\frac{3mol\lbrack OH^-\rbrack^{}}{1^{}molFe(OH)_3} \\ \\ \lbrack OH^-\rbrack=(8.1\cdot10^(-10)mol\lbrack OH^-\rbrack)/(L) \end{gathered}`

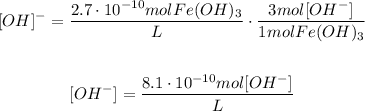
Now that we obtained each ion concentration, we could use the formula for Ksp:

`\begin{gathered} K_(sp)=\lbrack Fe^(3+)\rbrack^1\cdot\lbrack OH^-\rbrack^3 \\ K_(sp)=(2.7\cdot10^(-10)_{})^1\cdot(8.1\cdot10^(-10))^3 \\ K_(sp)=1.43489\cdot10^(-37)\approx0 \end{gathered}`

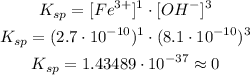
Thus, the ksp value for Fe(OH)3 given that that solubility is 2.7x10^-10mol/L is:

`K_(sp)=1.43489\cdot10^(-37)\approx0`