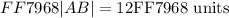Question

Find the distance between A(9, 3) and B(-3, 3) to the nearest hundredth

Answer 1

We are given two points in a cartesian coordinate system as follows:

`A\text{ ( 9 , 3 ) ; B ( -3 , 3 )}`

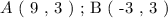
We are to determine the distance between points A and B.

The distance formula for cartesian coordinate plane is given as:

`|AB|=√((x_2-x_1)^2+\left(y_2-y_1\right)^2)`

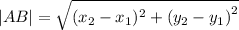
Where,

`\begin{gathered} A\colon(x_1,y_1)\text{ = ( 9 , 3 )} \\ B\colon(x_2,y_2)\text{ = ( -3 , 3 )} \end{gathered}`

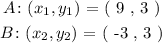
We will go ahead an plug the respective coordinates in the distance formula for AB as follows:

`\begin{gathered} |AB|=√((-3-9)^2+\left(3-3\right)^2) \\ |AB|=√((-12)^2+\left(0\right))\text{ = }√(12^2) \\ |AB|=\text{ 12 units} \end{gathered}`

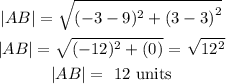
Since, the distance between points A and B is an integer; hence, the answer to nearest hundredth would be:

`\textcolor{#FF7968}=12\text{\textcolor{#FF7968}{ units}}`