Question

Rewrite the expression in terms of the given angle's reference angle: then evaluate the result. Write the exact answer. Do not round19COS

Answer 1

First, we'll convert the angle into degrees. We'll do so by replacing pi by 180, as following:

`(19\pi)/(4)\rightarrow(19\cdot180)/(4)\rightarrow855`

This way, we'll get that the angle is 855°. To this angle, we'll substract the nearest factor of 360: 720

`855-720=135`

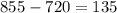
This way, we get an angle we can work on (between 0° and 360°)

Now, notice that 135° is an angle that belongs to the second quadrant. Because of this, we'll habe to substract 90° to get the reference angle:

`135-90=45`

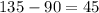
We get that the reference angle is 45°. Now, let's switch this angle back into radians. To do so, we multiplty by pi and divide by 180, as following:

`45\cdot(\pi)/(180)=(\pi)/(4)`

This way, we'll have that the reference angle for

`(19\pi)/(4)`

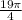
is:

`(\pi)/(4)`

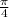
And since cosine is negative in the second quadrant (where the original angle belongs), we can conclude that:

`\cos ((19\pi)/(4))=-\cos ((\pi)/(4))`

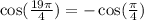
And we'll have that:

`-\cos ((\pi)/(4))=-\frac{\sqrt[]{2}}{2}`