We are given the details for downloads of songs of two size categories.
The first is a standard size which is 2.5MB. The second one is a high quality version which is 4.8MB.
Note that we do not know how many of each was downloaded (at least not yet). however, we do know that the total download for both category sizes was a total of 1060 songs. In other words
Standard size plus High quality size = 1,060.
We shall now assign variables to both categories;
Let standard size be letter a
Let High quality size be letter b.
For a total download size of 3593 MB in all, we can determine that;
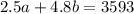
We can now set up a system of equations which are as follows;
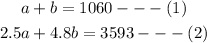
Note that in equation (1), what we've done is add up standard size and high quality size and that means a total of 1060 songs (regardless of its size/category).
We can now solve the following by means of the substitution method;
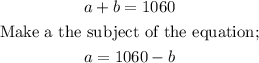
Now we substitute for the value of a into equation (2);
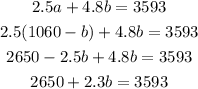
Next we subtract 2650 from both sides;
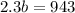
Next we divide both sides by 2.3;
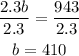
This means there were 410 downloads of the 4.8MB size.
We can now substitute the value of b into equation (1);
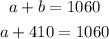
Subtract 410 from both sides;
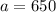
ANSWER:
There was 650 downloads of the standard version