Question

If someone walks along the outside of the garden from point A to point B, what percent of the garden’s border would they have walked around?

Answer 1

To solve for the length of arc AB, we need to know the measurement of the central angle that subtends it.

We know the following property:

Solving for x, we get:

`\begin{gathered} 70=(1)/(2)(50+x) \\ \\ 140=50+x \\ \\ 90=x \end{gathered}`

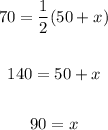
So we now know that arc DC meaures 90 degrees.

But arc DC is equal to m∠DYC, and m∠DYC = m∠EYB because they are vertical angles. m∠EYB = arc EB. Therefore arc EB measures 90 degrees.

arc EB = arc EA + arc AB

90 = 50 + arc AB

So arc AB = 90 degrees

We can now use this to solve the length of the arc.

`\begin{gathered} Arclength=2\pi r((\theta)/(360)) \\ \\ AB=100\pi((90)/(360)) \\ \\ AB=78.54 \end{gathered}`

People would have to walk 78.54 units to move from point A to point B along the outside of the garden.