Question

Express the function as a function of an acute angle:A) tan 110 degrees B) cos 200 degrees

Answer 1

Hello there. To solve this question, we'll have to remember some properties about trigonometric functions and sum of angles.

Given the following functions, we want to express them as a function of an acute angle:

`\begin{gathered} \tan(110^(\circ)) \\ \\ \cos(200^(\circ)) \\ \end{gathered}`

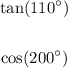
First, remember the following properties:

`\begin{gathered} \tan(\alpha+90^(\circ))=-\cot(\alpha) \\ \\ \cos(\alpha+\pi)=-\cos(\alpha) \\ \end{gathered}`

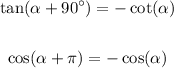
That we can prove easily knowing some properties of sum of angles:

`\begin{gathered} \tan(\alpha+90^(\circ))=(\sin(\alpha+90^(\circ)))/(\cos(\alpha+90^(\circ))) \\ \\ \text{ Whereas }\sin(\alpha+90^(\circ))=\cos(\alpha)\text{ and }\cos(\alpha+90^(\circ))=-\sin(\alpha) \\ \\ \text{ Therefore} \\ \\ \tan(\alpha+90^(\circ))=(\cos(\alpha))/(-\sin(\alpha))=-\cot(\alpha)_{\text{ }\square} \\ \\ \\ \end{gathered}`

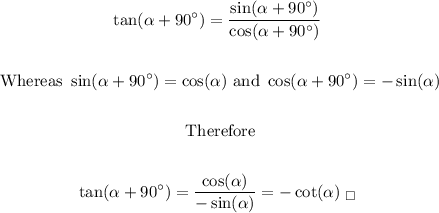
For the second, we use the same formula for sum of angles for cosines

`\begin{gathered} \cos(\alpha+180^(\circ))=\cos(\alpha)\cos(180^(\circ))-\sin(\alpha)\sin(180^(\circ)) \\ \\ \text{ But }\cos(180^(\circ))=-1\text{ and }\sin(180^(\circ))=0 \\ \\ \text{ Hence} \\ \\ \cos(\alpha+180^(\circ))=-\cos(\alpha)\text{ }_(\square) \\ \\ \\ \\ \\ \end{gathered}`

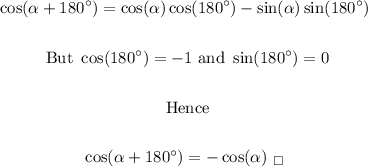
In this case, notice that

`\tan(110^(\circ))=\tan(\alpha+90^(\circ))`

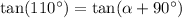
It is easy to see that

`\alpha=20^(\circ)`

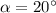
Such that the function expressing this as a function of an acute angle is

`-\cot(20^(\circ))`

And for the cosine, we'll get

`\cos(200^(\circ))=\cos(\beta+180^(\circ))`

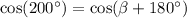
Again we see that

`\beta=20^(\circ)`

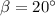
Such that we get the function

`-\cos(20^(\circ))`

There are the answer to this question.