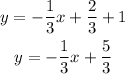Answer:
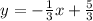
Step-by-step explanation:
Given the line y=3x+4
Comparing it to the slope-intercept form, y=mx+b
• Slope of y=3x+4 = 3
Two lines are perpendicular if the product of their slopes is -1.
Let the slope of the new line = m
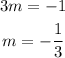
The slope of the perpendicular to the given line that goes through (2,1) is:
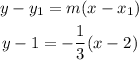
We then write it in slope-intercept form.