Given the equations:
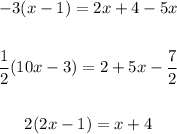
Let's evaluate each equation.
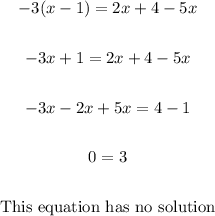


The statement that explains a way you can tell the equation has no solutions is:
It is equivalent to an equation that has the same variable terms but different constant terms on either side of the equal sign.
ANSWER:
Equation that has no solution: -3(x-1)=2x+4-5x
It is equivalent to an equation that has the same variable terms but different constant terms on either side of the equal sign.