Question

If you owe $50,000.00 at a 5% interest rate you are paying off over twentyyears, how much money will you pay each month? Search your way for thisanswer329.98

Answer 1

This problem seems to be about simple interest rates, which is defined by the formula

`P=(a)/(((1+r)^n-1)/(r(1+r)^n))=(a\cdot r(1+r)^n)/((1+r)^n-1)`

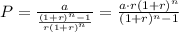
Where P refers to the payment per month, r refers to the interest rate (divided by the number of months per year), t is time in years, n is the number of periods per year.

This formula is about amortized loan payments.

According to the problem, the final amount is unknown, the principal is $50,000.00, the interest rate is 0.05 (5%) and the time is 20 years. So, we need to substitute each value in the formula to find the amount we'll pay after the interest

`P=(50000\cdot0.004166666(1+0.004166666)^(240))/((1+0.004166666)^(240)-1)=329.98`

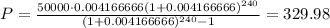
This means we are gonna pay back $329.76 per month.

It's important to consider that the rate r is found by dividing the interest 0.05 and the total months per year which are 12

`(0.05)/(12)=0.041666666666\ldots`

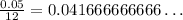
As you can observe, this is an infinite decimal number, so we take many decimal numbers as we need to get 329.98.