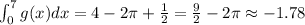Question

The graph of g consists of two straight lines & a semi circle….

Answer 1

ANSWERS

a) 3

b) -6.28

c) -1.78

Step-by-step explanation

The value of the integral of a function is the area "under" the graph of the function. It is usually called the area under, but it is the area between the curve and the x-axis.

a) The graph of the function between x = 0 and x = 1 is a straight line, and it forms a rectangle with a triangle on top,

The area under the curve is the sum of the areas of each shape.

The rectangle's base is 1 unit and its height is 2 units. The triangle's base is the same as the rectangle, 1 unit, and its height is also 2 units.

`\int ^1_0g(x)dx=A_(rec\tan le)+A_(triangle)=(1\cdot2)+(1\cdot2)/(2)=2+1=3`

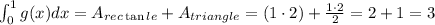
b) Between x = 2 and x = 6, the graph of the function is a semicircle with radius 2, so the integral of g(x) between 2 and 6 is the area of the semicircle, but since it is below the x-axis, we have a negative area,

`\int ^6_2g(x)dx=-A_(semicircle)=-(1)/(2)\pi r^2=-(1)/(2)\pi\cdot2^2=-(1)/(2)\pi\cdot4=-2\pi\approx-6.28`

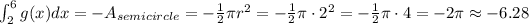
c) Now we have to find the area under the curve for the domain. Since the graph has different shapes between 0 and 7, we can split this integral with the intervals of each shape,

`\int ^7_0g(x)dx=\int ^2_0g(x)dx+\int ^6_2g(x)dx+\int ^7_6g(x)dx`

The second integral is the one we found in part b. The first integral is the area of the first triangle in the graph. Its base is 2 units and its height is 4 units,

`\int ^2_0g(x)dx=(2\cdot4)/(2)=4`

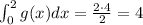
And the last integral is also the area of a triangle, but its base is 1 unit and its height is 1 unit,

`\int ^7_6g(x)dx=(1\cdot1)/(2)=(1)/(2)`

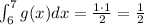
The result of the integral of g(x) between 0 and 7 is,

`\int ^7_0g(x)dx=4-2\pi+(1)/(2)=(9)/(2)-2\pi\approx-1.78`