eThe table of the observation is shown below:
Using a graphing calculator, the graph is plotted as shown below:
QUESTION 1:
The regression function that models the results can be gotten by checking the parameters of the graph as provided by the graphing calculator. These are shown below:
If the general form of an exponential function is given to be:
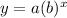
From the parameter. we have:
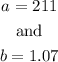
Therefore, the regression function will be:
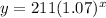
QUESTION 2:
The bacteria count at the beginning of the experiment can be gotten at x = 0. Therefore, we make this substitution into the regression function:
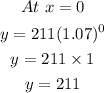
Therefore, the bacteria count will be 211.
QUESTION 3:
The growth rate in an exponential function is represented by r, if the function is given to be:
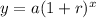
Comparing with the equation we used above, we have that:
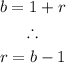
Substituting for b = 1.07, we have:
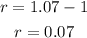
In percent, the rate will be:
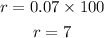
The growth rate is 7%.