Exponential growth model common ratio is defined as:
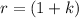
k is the growth rate written in decimals.
Given data:
Pn is the predicted number of speeding tickets during the year 2012+n
P0: 240 (First term)
Growth rate: 15% (0.15)
Then, the common ratio (r) is:
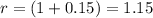
Recursive formula:
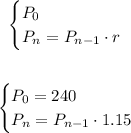
Explicit formula:
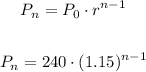
If this trend continues, how many speeding tickets are predicted to be issued in 2027:
Identify the value of n corresponding to year 2027:
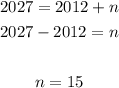
Find the predicted number of speeding tickets during the year 2012+15:
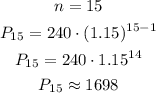
Then, in year 2027 the number of speeding tickets is: 1698