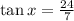Given:
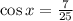
we know that:
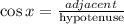
So, the adjacent side to x = 7 and the hypotenuse = 25
We can calculate the opposite side by the Pythagorean theorem
So, the opposite side will be:
![\sqrt[]{25^2-7^2}=\sqrt[]{625-49}=\sqrt[]{576}=24](https://img.qammunity.org/2023/formulas/mathematics/college/byzvy03f5zpmhivnsf59tzcg7oyzc80s5j.png)
So, tan x will be:
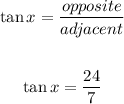
Another solution:
We know that:
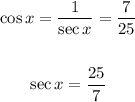
using the Pythagorean trig identity
![\begin{gathered} \tan ^2x+1=\sec ^2x \\ \tan ^2x=\sec ^2x-1=((25)/(7))^2-1=(625)/(49)-1 \\ \\ \tan ^2x=(576)/(49) \\ \\ \tan x=\sqrt[]{(576)/(49)}=(24)/(7) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jbbp16iszjbvyn0h43c3xlkabmo110xujr.png)
So, the answer will be: