Question

I’m confused about part 3a. Can you explain it to me conceptually?

Answer 1

Step-by-step explanation:

Spring plus a sphere is shown in the free body diagram below

we know that spring obeys hook's law

that is given by

`F=-kx`

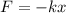
here, F is the applied force, k is the spring constant and x is compression or elongation in the spring. negative sign shows that spring force always acts in the negative direction.

From the free-body diagram

for the first position, we can see that compression in the spring is small

to press the sphere against the spring we apply some force

`F_1=10\text{ N}`

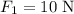
we assume that spring is compressed by some value say

`x=0.01\text{ m}`

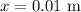
then from the hook's law, we can write

`\begin{gathered} k=(F_1)/(x) \\ k=\frac{10\text{ N}}{0.01\text{ m}} \\ k=1000\text{ N/m} \end{gathered}`

Similarly at position B we apply some greater force say

`F_2=20\text{ N}`

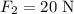
and spring compressed by some value say

`x=0.02\text{ m}`

then, from the hooks' law

`\begin{gathered} k=\frac{20}{0.02\text{ m}} \\ k=\text{ 1000 N/m} \end{gathered}`

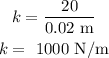
as we can see that there is a linear relationship between F and x.

Similarly for position A can also be understood.

we can also use energy conservation here

`P.E=K.E`
`(1)/(2)kx^2=(1)/(2)mv^2`

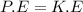
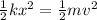
the more we pressed the sphere against the spring the fast it moves.

this method will also give the same value of spring constant provided you correctly measure the speed of the object after released.