Question

In a certain country, the probability that a baby that is born is a boy is 0.52 and the probably that a baby that is born is a girl is 0.48. A family has two children. If X is the number of girls born to a family, find the probability that the family has 0, 1, or 2 girls.

Answer 1

Given:

In a certain country, the probability that a baby that is born is a boy is 0.52 and the probably that a baby that is born is a girl is 0.48. A family has two children.

Required:

To find the probability that the family has 0, 1, or 2 girls.

Step-by-step explanation:

Let B=boy and G=girl.

Probability of 2B is,

`\begin{gathered} =(0.52)(0,52) \\ =0.2704 \end{gathered}`

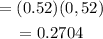
Probability of BG is

`\begin{gathered} =(0.52)(0.48) \\ =0.2496 \end{gathered}`

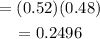
Probability of GB is the same as the probability of BG, so it is 0.2496.

Probability of 2G is

`\begin{gathered} =(0.48)(0.48) \\ =0.2304 \end{gathered}`

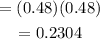
Here is the tree for part (a),

0 child 1st child 2nd child

| -- Boy (27.04%)

_ Boy (52%) -------[

Start | | -- Girl (24.96%)

X -------------------|

| | -- Boy (24.96%)

|_ Girl (48%) --------[

|_ Girl (23.04%)

Final Answer:

0 child 1st child 2nd child

| -- Boy (27.04%)

_ Boy (52%) -------[

Start | | -- Girl (24.96%)

X -------------------|

| | -- Boy (24.96%)

|_ Girl (48%) --------[

|_ Girl (23.04%)