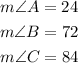Question

3 pts In AABC, mZA = r°, mZB = 3.rº, and mZC = Find the measures of the three angles. (4x – 12) mLA = mZB mZC

Answer 1

On any triangle, the sum of the measures of the internal angles is 180°. Then:

`m\angle A+m\angle B+m\angle C=180`

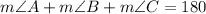
Substitute the expressions for each angle, solve for x and find the measure of each angle:

`\begin{gathered} \Rightarrow x+3x+4x-12=180 \\ \Rightarrow8x-12=180 \\ \Rightarrow8x=180+12 \\ \Rightarrow8x=192 \\ \Rightarrow x=(192)/(8) \\ \Rightarrow x=24 \end{gathered}`

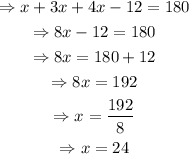
To find the measure of each angle, substitute x=24 into the expressions:

`\begin{gathered} m\angle A=x \\ \Rightarrow m\angle A=24 \end{gathered}`
`\begin{gathered} m\angle B=3x \\ \Rightarrow m\angle B=3(24) \\ \Rightarrow m\angle B=72 \end{gathered}`
`\begin{gathered} m\angle C=4x-12 \\ \Rightarrow m\angle C=4(24)-12 \\ \Rightarrow m\angle C=96-12 \\ \Rightarrow m\angle C=84 \end{gathered}`

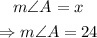
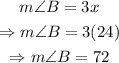
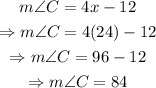
Therefore, the measures of the three angles are:

`\begin{gathered} m\angle A=24 \\ m\angle B=72 \\ m\angle C=84 \end{gathered}`