Question

The two triangles above are similar. a. Find x using the ratio of the sides 12 cm and 16 cm: x/20=12/16. Show your work. b. Find x using the ratio of the sides 6 cm and 8 cm. Show your work. c. Explain why the answer to (a) and (b) should be the same.

Answer 1

a)

If the triangles are similar, the corresponding sides vary on the same proportion, so the ratios between the corresponding sides are equal.

For

`(x)/(20)=(12)/(16)`

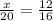
To solve for x you have to multiply both sides of the expression by 20

`\begin{gathered} (20x)/(20)=((12)/(16))\cdot20 \\ x=((3)/(4))\cdot20 \\ x=15 \end{gathered}`

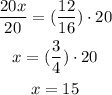
b)

Following the same logic, the ratio between x and 20 is the same as the ratio between 6 and 8

`(x)/(20)=(6)/(8)`

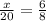
6/8 can be simplifies as 3/4. Then multiply both sides by 20 to determine the value of x.

`\begin{gathered} (x)/(20)=(6)/(8) \\ 20\cdot(x)/(20)=((3)/(4))\cdot20 \\ x=15 \end{gathered}`

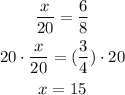
As mentioned above, when two triangles are similar, the corresponding sides are always in the same ratio, that is why the results in a and b are the same.