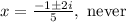For a quadratic function

The x-coordinates for the roots can be found using the Bhaskara formula:
![x=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/wyc1fg1v8a6l4tr8e7zi6v658dpql32brp.png)
So, to solve this question, follow the steps below.
Step 01: Find a, b and c.
For the equation
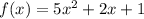
a = 5
b = 2
c = 1
Step 02: Substitute the values in the Bhaskara formula to find x.
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2a} \\ x=\frac{-2\pm\sqrt[]{2^2-4\cdot5\cdot1}}{2\cdot5} \\ x=\frac{-2\pm\sqrt[]{4-20}}{10} \\ x=\frac{-2\pm\sqrt[]{-16}}{10} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6xm76yfkiipr4nwax4umunhiaxn7h3f6lr.png)
Since i² = -1, you can substitute -16 by 16*i²:
![\begin{gathered} x=\frac{-2\pm\sqrt[]{16\cdot i^2}}{10}=\frac{-2\pm\sqrt[]{16}\cdot\sqrt[]{i^2}}{10} \\ x=(-2\pm4\cdot i)/(10) \\ x=(-1\pm2i)/(5) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/cq5qky5hwrm2vrduny73fit89osispehpx.png)
The roots are:
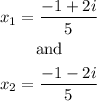
Step 03: Evaluate where the equation crosses the x-axis.
When the value inside the root is negative, it means that the equation does not cresses the x-axis.
Also, you can graph the equation to observe it:
Answer: