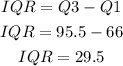Question

find the value for the given set of numbers.Mean:Median:Mode:Minimum:Maximum:Lower Quartile:upper Quartile:Range:Interquartile Range:

Answer 1

Mean: 80.923

Median: 82

Mode: 84

Minimum: 58

Maximum: 104

Lower Quartile: 66

Upper Quartile: 95.5

Range: 46

Interquartile Range: 29.5

Explanation

The mean is found as follows:

`\begin{gathered} mean=\frac{sum\text{ of values}}{number\text{ of values}} \\ mean=(98+84+62+68+100+104+75+80+93+82+58+64+84)/(13) \\ mean=(1052)/(13) \\ mean\approx80.923 \end{gathered}`

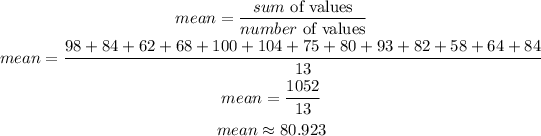
To find the median and some other parameters, first, we need to order the list of values from least to greatest.

The median is the value placed in the middle of the ordered list.

The lower quartile (Q1) is the value placed in the middle from the minimum to the median. In this case, there are two values, then Q1 is the average between them.

The upper quartile (Q3) is the value placed in the middle from the median to the maximum. In this case, there are two values, then Q3 is the average between them.

The mode is the most frequent number. In this case, all the values have a frequency of 1 except 84 which has a frequency of 2, then it is the mode.

The range of data is calculated as follows:

`\begin{gathered} range=maximum-minimum \\ range=104-58 \\ range=46 \end{gathered}`

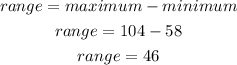
The interquartile range (IQR) of data is calculated as follows:

`\begin{gathered} IQR=Q3-Q1 \\ IQR=95.5-66 \\ IQR=29.5 \end{gathered}`