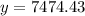Question

Instructions: Create the equation of the form y=a(b)x for the exponential function described in each real-world problem. Then, use the equation to answer the question.

Answer 1

Since the number of bacterial increases then this shows an exponential growth function:

The function is defined as

`y=a(1+r)^x`

The initial value is 113 and the rate is 82% hence the equation becomes

`\begin{gathered} y=113(1+82\%)^x \\ y=113(1+0.82)^x \\ y=113(1.82)^x \end{gathered}`

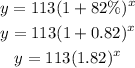
Therefore the equation is of the form

`y=113(1.82)^x`

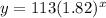
To find the number of bacteria after 7 days substitute x=7 into the equation

This gives

`\begin{gathered} y=113(1.82)^7 \\ y=7474.43 \end{gathered}`

Therefore the value of y is

`y=7474.43`