Solution:
A boxplot is a standardized way of displaying the dataset based on a five-number summary: the minimum, the maximum, the median, the first quartile, and the third quartile.
The general representation for a box plot is given below;
Comparing this to the box plot given in the question, the following can be deduced;
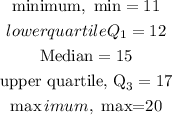
Therefore, the answer as arranged is;
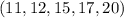
The interquartile range, IQR is given by;
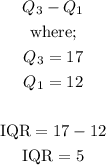
Therefore, the interquartile range is 5.