Question

Sharon Nguyen has $25,000 to invest and believes that she can earn 6% compounded semiannually. Find the compound amount if she invests for 10 years

Answer 1

In order to calculate the compound amount, we can use the formula below:

`A=P\cdot(1+(r)/(n))^(nt)`

Where A is the amount after t years, P is the principal (initial amount), r is the interest rate and n is how many times the interest is compounded in a year.

So, for P = 25000, r = 0.06, t = 10 and n = 2, we have:

`\begin{gathered} A=25000\cdot(1+(0.06)/(2))^(2\cdot10) \\ A=25000(1.03)^(20) \\ A=45152.78 \end{gathered}`

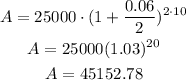
Therefore the amount after 10 years is $45152.78.