Answer:
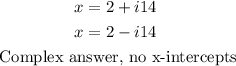
Step-by-step explanation: The discriminant is the part of the quadratic formula underneath the square root symbol As we know that square root of any number is both plus and minus of a certain value:
![\sqrt[]{a}=\pm c\Rightarrow(-c)^2=(+c)^2=a](https://img.qammunity.org/2023/formulas/mathematics/college/lto7wdo7yicf7kuwb5ukye9nxxv76hqbeo.png)
Using this information about the discriminant we can determine the x-intercepts of the graph as follows:
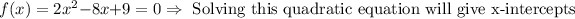
Quadratic equation solution:
![\begin{gathered} f(x)=2x^2-8x+9=0\Rightarrow x=\frac{-B\pm\sqrt[]{B^2-4AC}}{2A} \\ \because\Rightarrow \\ A=2 \\ B=-8 \\ C=9 \\ \therefore\Rightarrow \\ x=\frac{-(-8)\pm\sqrt[]{(-8)^2-(4*2*9)}}{2*(2)}=\frac{8\pm\sqrt[]{16^{}-72}}{4}=\frac{8\pm\sqrt[]{-56}}{4}=2\pm\frac{\sqrt[]{-56}}{4} \\ \therefore\Rightarrow \\ x=2\pm i14 \\ \rightarrow\text{ Complex answer} \\ x=2+i14 \\ x=2-i14 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jo5nkizq1lzk1eok08ma6mo6u65xa0p2rl.png)
Graph
Note! The plot of f(x) above confirms that there are no x-intercepts of this function, so the reason for complex values of x. also discriminant is the square root of -56