1 Answer

Tiago · Answer 1 · 2023-09-08T23:41:56+0000

The trigonometric functions tangent, sine and cosine are related by the following equation:

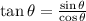
$\tan \theta=(\sin \theta)/(\cos \theta)$

In this case, the angle is y°, so:

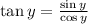
$\tan y\degree=(\sin y\degree)/(\cos y\degree)$

Since we want the cosine, we can solve for it ans substitute the given tangent and sine:

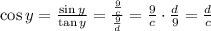
$\cos y\degree=(\sin y\degree)/(\tan y\degree)=((9)/(c))/((9)/(d))=(9)/(c)\cdot(d)/(9)=(d)/(c)$

This corresponds to the third alternative.

Please log in or register to add a comment.