ANSWER
36°
Step-by-step explanation
Let a and b be the measures of the two angles. We know that they are complementary, so their measures add up to 90°. Also, we know that the quotient between their measures is 2/3,
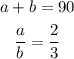
Solve the second equation for a,
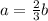
Replace a with this expression in the first equation,
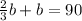
Add like terms,
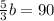
Solving for b,

So the other angle is,

Hence, the measure of the smaller angle is 36°.